Geometry, and the Role it Plays in Leaf Arrangements
When nature and mathematics intertwine, the result is a marvel
I get excited when mathematics occur in the world of botany.
Recently, a friend of mine taught a class on Algorithmic Botany at SFPC, and it had been the first time that I was introduced to the concept while also having a lot of time on my hands.
I hear often that math is the language of nature, so having a comprehensive understanding of how math appeared in the wild seemed useful info to have, if the efficiency is beauty reasoning wasn’t enough.
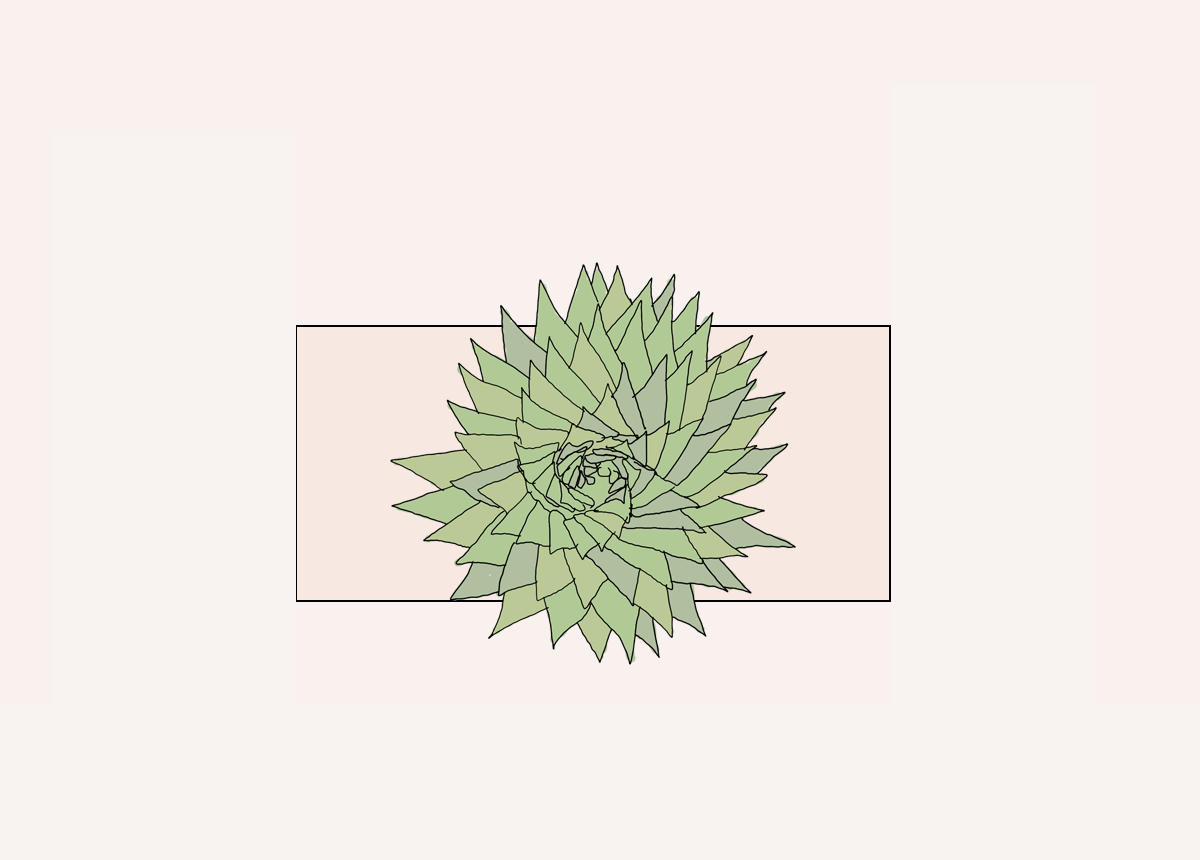
One of the more documented phenomena of math and beauty is the idea of a phyllotaxis pattern where leaves spiral from the center as they grow outward. Fun fact, the word is derived from Greek, where "phyllon" means leaf, and "taxis" means arrangement.
Like I said, I have a lot of time, so sure, I’m down for a little math. Let’s explore.
The Mathematics of the Spiral Phyllotaxis
The spiral phyllotaxis pattern can be represented using what people are calling ‘the golden angle’, which is approximately 137.5 degrees.
We start in the middle and gradually fan out, each new leaf approximately separated by the golden angle. This angle ensures that new growth, be it a leaf or seed, is optimally spaced from the ones before it, ensuring maximum package of objects, at least in a spiral.
With this arrangement, every leaf/seed/etc supposedly gets maximum exposure to sunlight and air without overshadowing its neighbors, something posited by Wilhelm Hofmeister in 1868. This is useful for plants, as they can photosynthesize more efficiently, which means, in some cases, more food for us. Higher seed production yields versatility.
Moreover, other plants follow the phyllotaxis pattern, ensuring protective and efficient growth of whatever is stored in the center. In pineapples, the pattern aids in shielding the inner fruit while ensuring each segment gets enough sunlight and air. In pinecones, the efficient packing of scales, ensuring that each scale can grow to its full size without being obstructed by its neighbors.
It’s important to note that this spiral shape is not the default best way to packed things into a space. Rather, it’s as good as the other arrangements. And we know because researchers have already studied that.
Sunflower Seeds as a Concrete Example
Some people eat pinecones, but sunflower seeds are more common example. In sunflowers, seeds are arranged in spirals that radiate outwards. Like other examples of the spiral shape, this specific arrangement ensures that the sunflower produces a maximum number of seeds.
From a food production standpoint, seeds are rich in oil and nutrients, which, again, is useful. In fact, while most GMO’s are using focused on increasing resistance to pests, diseases, but genetic engineering could be aimed at growth patterns soon. In fact, ongoing research is taking place better understand the biochemical processes by which plants sculpt their leaf patterns.
So far, the leading theory is that the formation of primordial seeds is driven by high auxin concentrations. The growing seeds exert forces on each other, creating geometric patterns, and the geometry can trigger the production of auxin, leading to a feedback loop. It’s an interesting mix of biochemistry, mechanics and geometry.
Conclusion
Writing this blog taught me just how cool study of phyllotaxis patterns is. I had a feeling, but it’s nice for it to be confirmed.
In phyllotaxy, mathematics, biology, and food production come together in a nice little intersection that I can write about, so I’m sure I’ll write a few times more about this topic. It's a reminder that efficiency and beauty go hand in hand in the natural world.